Tilstandskontroll
Publisert: 16. april 2013
Oppdatert: 4. februar 2025
1 Tilstandskontroll og sporkvalitet
1.1 Et spors kvalitet
1.1.1 Definisjoner
Et spors kvalitet er bestemt av hvor liten del av sporet som beheftet med feil i høyde- og sideretning, og for å forbedre sporkvaliteten, må vi derfor foreta sporjusteringer. Justeringen har som formål å opprettholde en gitt beliggenhet og tilstand for sporet ved å utbedre feilene, samt å stabilisere sporet.
Hva er så feil i sporet? I første omgang tenker vi på geometriske feil i størrelsesorden fra noen få millimeter, typisk avdekket under målevognskjøring, som blir et sentralt emne videre. I neste omgang kan sporets beliggenhet i et ytre referansesystem utgjøre feil vad sporet. Dersom sporets utfesting ikke er korrekt, vil dette være opphav til skinnespenninger/ikke nøytralisert spor og eventuelle konflikter mellom sporet og fastpunkter i sporet/andre objekter.
I det følgende skal vi konsentrere oss om den sporkvaliteten som fremkommer ved å kontrollere og eliminere sporgeometriske feil. Potensielle feil ligger imidlertid i mangelen på kontroll av sporets beliggenhet gjennom utfesting, som igjen vil gi en dårlig kvalitet på sporet.
1.1.2 Krav til utførelse av sporjustering
Gjennomgående sporjustering skal foretas maskinelt, enten helautomatisk eller ved manuelt innleste data beregnet utfra teoretisk beliggenhet og beregnede justeringsdata.
På K0-baner skal det, i tillegg til utfesting med GVUL, benyttes arbeidsmaskiner med laser, optisk nivellement/løft eller tilsvarende utstyr. På øvrige baner kan slikt utstyr med fordel benyttes.
1.1.3 Målinger av sporets geometri og kvalitet
Grunnlag for vurdering om sporjustering er påkrevet er data fra målevogn. Sporgeometrien skal måles iht. frekvenser angitt i tabellen under. Tallene i parentes gjelder strekninger med strekningshastighet 200 km/h.
| Kvalitesklasse | Hastighet (km/h) | Antall målevågnkjøringer pr. år | |
|---|---|---|---|
| Sporgeometri | Sporkvalitet | ||
| K0 | 205– | 6 | 4 |
| K0 | 145–200 | 4 | 2 |
| K1 | 125–140 | 2 | 2 |
| K2 | 105–120 | 2 | 2 |
| K3 | 75–100 | 2 | 2 |
| K4 | 40–70 | 1 | 11) |
| K5 | –35 | 1 | – |
1 Gjelder kun hovedspor.
1.1.4 Krav til kontroll i forbindelse med sporarbeider
Etter Bane NORs tekniske regelverk gjelder at:
Kontroll av sporets geometri skal foretas i følgende tilfeller:
- I grovjusterte sporavsnitt etter utførelse av arbeider, før og etter første togpassering.
- I grovjusterte sporavsnitt hvor det senere oppdages tendenser til lokale setninger av sporet.
- Etter grovjustering minst én gang hver tredje dag. Hyppigere kontrollfrekvens bør gjennomføres ved særskilte forhold som høy trafikkbelasting, høyre tempraturer og storenedbørsmengder. Dette gjelder inntil sporet er pakket med skinnegående justeringsmaskin.
- I finjustert sporavsnitt etter utførelse av arbeider, før første togpassering.
- Etter utbedring av solslyng.
1.2 Målevognskjøring
1.2.1 Generelt
Resultater fra målevognskjøring er i dag den viktigste kilden til kontroll av sporets tilstand. Utfra tolkning av målevognsdiagrammer kan vedlikeholdsbehovet kartlegges.
Det finnes flere grunner til å foreta kontroll av sporet:
- Planlegge vedlikeholdsarbeid
- Kontrollere at vedlikehold spor oppfyller kvalitetskravene
- Spesielle måleoppgaver
En prinsipiell fordel ved å anvende målevogn er at sporet måles under belasting tilnærmet lik den alminnelig togtrafikk.
I tillegg til målevognskjøring utføres også manuelle målinger. I spor som er utfestet i et geodetisk referansesystem, blir også sporets absolutte beliggenhet målt inn. Målevognskjøringen er kun målinger relatert til sporet.
Målevågenes resultat viser som regel både sporets geometri og avvik fra ønsket geometri. Komfortmålinger er derimot lite utbredt.
1.2.2 Historikk
De første målingene i sporet ble utført med Hallades apparat i 1925, som vha. bl.a. tre pendler tegnet et diagram der en kunne tolke ujevnheter i sidebeliggenhet og overhøyde. Målingene viste ikke geometri direkte, men var mer et mål på komforten, slik at ukomfortabel toggang indikerte dårlig tilstand på sporet.
Pilhøydemålinger ble vanlig på 1920-tallet, slik at justering av kurver ble lettere. I 1929 ble en målevogn bygget i Tyskland som kunne måle overhøyde, side- og høydebeliggenhet i opptil 100 km/h.
På 1930-tallet bygde overingeniør M. Mauzin sin første målevogn, og etter krigen ble disse satt i fransk produksjon. Vognene ble også utleid, bl.a. til Sverige og Norge, og i 1958 bygget SJ sin egen Mauzin-vogn (målesystemet ble egentlig bygget av Matisa), som i Danmark og Norge ble leietakere av helt fram til 1990-tallet. Vogna, som ble koblet inn i vanlige tog, kunne måle med en hastighet på opptil 130 km/h, og på 1980-tallet ble systemet oppgradert med datamaskiner for å kunne levere tilleggsdokumentasjon utover det alminnelige diagrammet. Vogna ble museumsgjenstand i 1996.
Andre målevogner ble også utviklet på 1960- og 1970-tallet, som Matisa PV6, PV7 og Plasser & Theurer EM50 og EM80, og Norge har både kjøpt og leid (fra Sverige) flere av disse. Disse vognene er imidlertid ofte langt mindre og kan bare måle i hastigheter opptil 80–90 km/h.
Felles for alle målevognene ev 1. generasjon slik som beskrevet over, er at de langt på veg er helt mekaniske. Dette vil si at alle mekaniske forskyvninger/bevegelser, som skyldes ujevnheter i sporet, overføres mekanisk til et tegnebord eller tilsvarende vha. et sinnrikt system av hjul, trinser, kjeder og vaiere. Først på nyere modeller registreres måledata elektronisk utfra opprinnelig mekanisk målte parametre.

1.2.3 Dagens måleutstyr
I 1997 tok Banverket i Sverige i bruk sin nyeste målevogn STRIX som erstatning for Mauzin-vogna. STRIX er en 2. generasjons målevogn idet den hovedsaklig anvender et såkalt treghetssystem for sporgeometrimålinger. Størsteparten av målingene stammer derfor fra en komplisert prosessering av data målt av akslerometre. Vogna kan måle i opptil 160 km/h. STRIX leverte de offisielle hovedmålingene på JBVs banenett fra 1997 til 2001.
JBV besluttet i 1996 å anskaffe sin egen målevogn, som er bygget hos italienske MerMec og ble levert Jernbaneverket i 2000: ROGER 1000. Vogna er en hybridløsning og kan måle i opptil 200 km/h innsatt i en togstamme og 160 km/h som selvgående motorvogn. ROGER 1000 kan kalles en 3. generasjons målevogn: foruten å inneholde flere målesystemer enn bare sporgeometri, er en stor del av datainnsamlingen basert på laseroptikk. Tekniske detaljer rundt målesystemet i ROGER 1000 vil ikke bli nærmere beskrevet her, men en oversikt over målesystemene om bord er beskrevet under.

ROGER 1000 består av et integrert målesystem med følgende fire delmålesystemer:
- Sporgeometri
- Skinneprofil – for utregning av vertikal og horisontal skinneslitasje
- Rifler og bølger på skinnehode
- Kontaktledningen – kraft, høyde, og sikk-sakk, i tillegg digitalvideo av ledningen
Målesystemet for sporgeometri, som i første omgang er det som angir sporkvalitet, er basert på 8 basisparametre. Disse er de samme som fantes på Mauzin-vogna og som vanligvis måles av de aller fleste vogner, som regel for hver kvarte eller halve meter. De ulike parametrene som måles av delsystemet for sporgeometri er listet nedenfor og vil bli gjennomgått i neste avsnitt som sporgeometriske feil:
- Sporvidde
- Vindskjevhet
- Høydefeil, venstre og høyre skinne
- Overhøyde
- Horisontaltkurvatur/pilhøyde på 10 m basis
- Sidefeil, venstre og høyre skinne
1.3 Sporgeometriske feil
1.3.1 Sporvidde
Sporvidden er det vinkelrette mål mellom kjørekantene målt 14 mm under sporplan. Sporviddens grunnverdi er 1435 mm.
1.3.1.1 Årsaker til avvik i sporvidden
Økning i sporvidden forårsakes av:
- at befestigelsen gir etter på tresviller
- slitasje av isolatorer på betongsviller
- skinneslitasje
Reduksjon av sporvidden forårsakes av:
- utvalsing av skinnehodet
- forandring av svillens beliggenhet (skjeve sviller)


1.3.1.2 Konsekvenser og toleranser
På steder der sporvidden er blitt 1470 mm eller større, skal utbedring foretas umiddelbart. Hastigheten reduseres inntil feilen er utbedret.
Sporvidden bør være så jevn som mulig. Store sporviddevariasjoner kan innvirke på sporets sidestabilitet. Sporviddens endring begrenser sporviddevariasjonen. Endringen regnes over 10 m sporlengde.
I kontrakurver uten overgangskurver med kort eller ingen mellomliggende rettlinje, skal sporutvidelser ikke være større enn en viss verdi. Når sporvidden er for stor, er det fare for ombufring, særlig under skyving av store togstammer.
I sporveksler gjelder egne toleranser for sporutvidelser for de ulike elementene innenfor vekselen.
1.3.1.3 Måling av sporvidde
Vi skiller mellom to metoder for måling:
- Manuell måling
- Målevognkjøring
Manuell måling foretas som regel når målevogna har avdekket avvik i sporvidde. Dette gjøres vha. et skinnemål, som vanligvis kan måle både sporvidde og samtidig overhøyde vha. et vater.

Det er viktig å være oppmerksom på at måling av sporvidden på hhv. belastet og ubelastet spor vil gi svært forskjellige resultat. dermed vil målevognskjøring som regel vise større sporutvidelser enn de manuelle målingene. I tillegg vil de målte sporutvidelsene også variere med hvilken målevogn som benyttes. Både aksellast, type målesystemet som anvendes og hvor målesystemet er montert under vogna vil ha en signifikant effekt. Tabell under viser aksellasten og målesystemet til noen målevogner som har blitt/blir benyttet pådet offentlige jernbanenettet:
| Målevogn | Aksellast [tonn] | Målesystem |
|---|---|---|
| Mauzin | 5 | mekanisk |
| PV7 | 6 | mekanisk |
| EM80 | 11 | mekanisk |
| STRIX | 11 | laseroptisk |
| ROGER 300 (MerMec) | 10 | laseroptisk |
| ROGER 1000 (MerMec) | 15 | laseroptisk |
En forskjell mellom mekaniske og laseroptiske systemer for sporviddemåling er at førstnevnte som regel vil måle den til enhver tid minste sporvidden mellom skinnestrengene, mens sistnevnte måler konsekvent 14 eller 15 mm under skinnetopp. Laseroptiske systemer kan derfor i noen tilfelle måle en større sporvidde enn virkelig som følger av for eksempel utvalsing av skinnen.
1.3.1.4 Utbedring av for stor sporvidde
For for stor sporvidde på tresviller som skyldes at underlagsplatene har gravd seg ned i svillen, kan utbedres ved innlegging av skoringsplater. Midlertidig utbedring kan foretas ved innskruing med strekkbolter. Strekkbolter skal ikke ligge i sporet mer enn 1 år. Dersom det ikke er mulig å justere sporvidden med skoring eller innskruing, må det foretas utskifting av svillene.
For stor sporvidde som skyldes slitasje av isolatorer utbedres ved a skifte ut isolatorer.
1.3.1.5 Utbedring av for liten sporvidde
For liten sporvidde som skyldes utvalsing av skinnehodet, kan utbedres ved høvling og eller sliping, ev. ved svilleregulering.
1.3.1.6 Eksempel på utvikling av sporutvidelse
Nedenfor følger et eksempel som viser sporutvidelser i vekst når ikke regelverkets krav har blitt overholdt. Utvidelsens lengder omfatter også den aktuelle kurvens overgangskurver.
Eksempelet er hentet fra en feilanalyse av en rekke kurver på Gjøvikbanen som opprinnelig ble påbegynt høsten 1998. Omfanget av feilene medførte da pålegg om målevognskjøring hver 14. dag!
I sammen tidsrom ble en todelt plan om sporbytte på mange av kurvene mellom Roa og Eina på Gjøvikbanen utarbeidet, og gjennom 1999 og 2000 fikk de mest utsatte kurvene (del 1) derfor flere av kurvene som ble analysert både nye skinner og sviller. Del 2 av planen for sporbytte ble imidlertid ikke fulgt opp før slutten av 2002/begynnelsen av 2003, og banen slet derfor i mellomtiden med til dels sikkerhetskritiske sporutvidelser i enkelte kurver, noe eksempelet under viser.
Vi ser at midlertidige tiltak først ble utført etter den pålagte ekstramålingen 06.11.98, der sporutvidelsene kommet under tiltaksgrensen. Det ble både benyttet strekkbolter og skoringsplater. Varigheten av tiltaket holdt imidlertid ikke lenge enn til at det ble målt tiltaksfeil igjen flere ganger i løpet av vinteren. Nye midlertidige tiltak ble gjennomført våren 1999, men sporutvidelsene var fortsatt like under tiltaksgrensen. Lengden på feilen var heller ikke redusert noe. Gjennom 2000 ble feilen igjen en tiltaksfeil, og senest i august 2002 passerte feilen sikkerhetsgrensen på 1470 mm.
Påfølgende vår- og høstmålinger fra 2003 utover imidlertid ikke vist sporvidder i kurven på over 1450 mm (vedlikeholdsgrensen) som forventet etter sporbytte.
1.3.1.7 Roa–Hønefoss (670) km 64,2325
| Trasedata | R = 247 m (høyre) | h =150 | L = 263 m |
|---|---|---|---|
| Skinnedata | 49-E1 | Stålkv. R200 | Innlagt 1976/Valseår 1960 |
| Svilledata | Bet-JBV97 FC | Pandrol Fastclip | Innlagt 2009 |
| Når | Maks. sporvidde [mm] | Lengde[m] |
|---|---|---|
| Vår 2014 | 1464,3 | – |
| Høst 2014 | 1464,9 | – |
| Vår 2015 | 1466,3 | 1,0 |
| Høst 2015 | 1467,5 | 6,5 |
| Vår 2016 | 1466,6 | 2,5 |
| Høst 2016 | 1468,2 | 7,5 |
| Vår 2017 | 1467,9 | 6,0 |
| Høst 2017 | 1468,6 | 9,0 |
| Vår 2018 | 1470,5 | 11,0 |
| Høst 2018 | 1472,3 | 12,5 |
1.3.2 Vindskjevhet
Et spor er vindskjevt når overhøyden varierer fra punkt til punkt i sporet som vist på figur under.
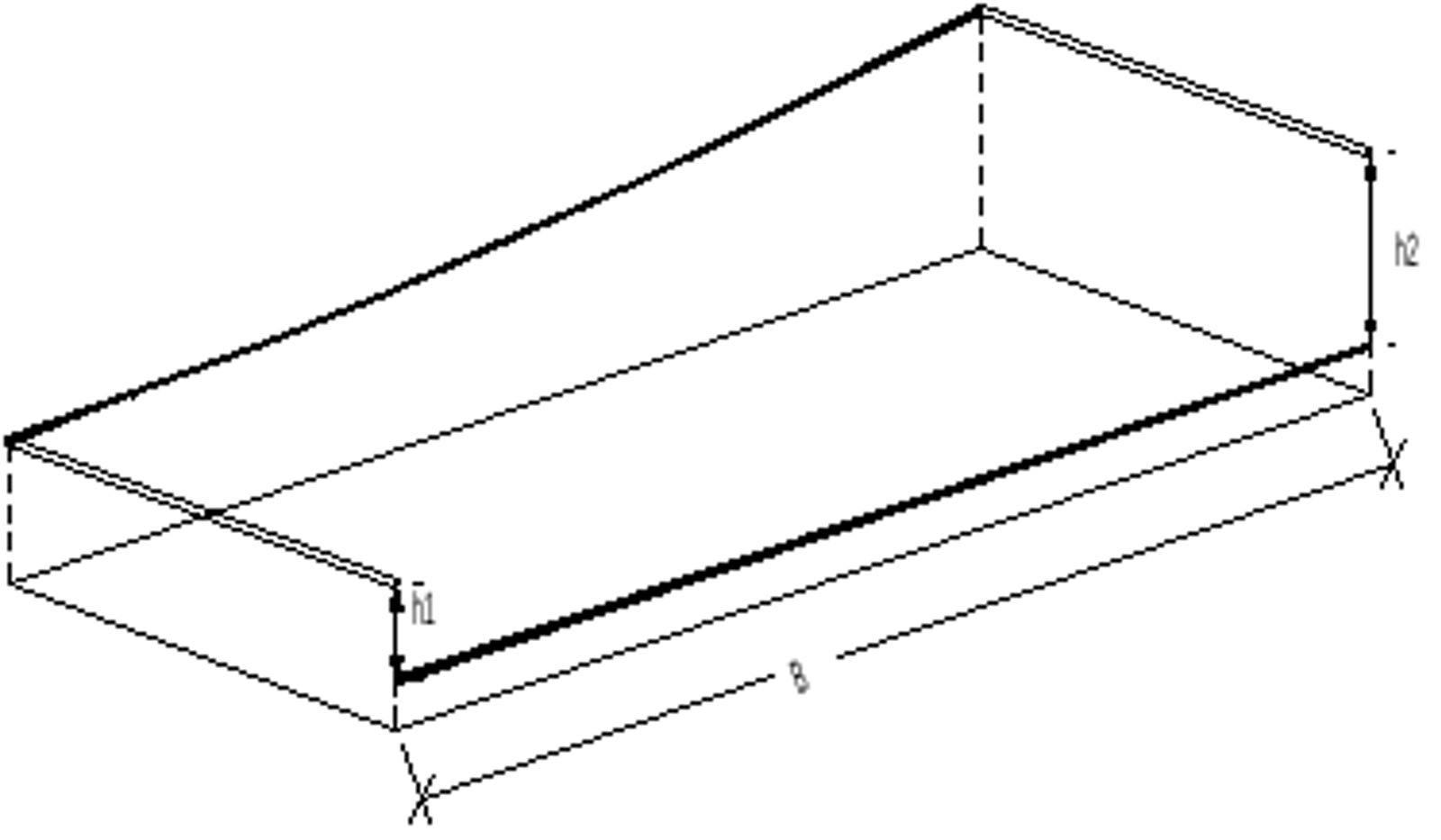
Vindskjevhet oppgis gjerne i mm, men dette må ses i forhold til den målebasis som anvendes. Helt korrekt enhet er enten mm/m eller ‰.
1.3.2.1 Årsaker til vindskjevhet
Vindskjevhet kan skyldes feil i skinnenes høydebeliggenhet eller være tilsiktet i forbindelse med overhøyderamper. Vindskjevhet som feil er som regel langt større enn den tilsiktede (rampestigning) og kan oppstå i spor med telefarlige masser, ustabiliserte spor og etter under gravearbeider.
1.3.2.2 Konsekvenser og toleranser
Størrelsen på den største vindskjevhet som finnes er i stor grad avhengig av lengden på målebasis. Dette er gjengitt i toleransene i promille (‰), som er strengere for 9 m enn for 2 m (3,4 ‰ kontra 5,0 ‰).
For å se på følgene på den største vindskjevt spor, er den stive vogna uten fjæring et godt utgangspunkt. Når denne går inn i en overgangskurve og opp en overhøyderampe fra en rettlinje, vil det fremre, ytre hjulet påvirkes av en økt kraft, mens den bakre, ytre hjulet vil avlastes – i det svært teoretiske tilfellet totalt. Ut av sirkelkurven igjen og ned en overhøyderampe skjer det motsatte – det fremre, yte hjulet avlastes.
For virkelig rullende materiell er situasjonen den samme, bare mer komplisert på grunn av materiellets dynamiske egenskaper og avhengig av hvor bratt den aktuelle rampa er. Som oftest finnes lokale, utilsiktede vindskjevheter innenfor rampa, som dermed må legges til den tilsiktede vindskjevhet. Hvis denne summen blir stor nok får det ytre hjulet avlasting nok til å klatre over skinnekanten og vi får avsporing. Det er altså i ramper med minkende overhøyde faren for avsporing er aller størst.
At toleransen for vindskjevheter målt på 9 m basis er lavere enn på 2 m basis er ikke tilfeldig. En del uønskede hendelser på Østlandet på 2000-tallet viser at vindskjevheter på 9 m basis trolig har vært medvirkende årsak til at toakslede godsvogner har sporet av. Avsporinger for boggimateriell forekommer derimot langt sjeldnere, og denne faren avdekkes gjennom måling av vindskjevheter på 2 m basis. Basert på gammel som helt fersk erfaring er overvåking av 9 m – feilene langt på veg viktigst av de to.
På steder der vindskjevheten måles til å være større enn 14 mm (7 ‰) over 2 m målebasis eller 43 mm over 9 m målebasis, skal justering foretas umiddelbart. Der den tilstøtende sirkelkurven har radius mindre enn 275 m, reduseres toleransen på 9 m basis til kun 35 mm.
1.3.2.3 Måling av vindskjevheter
Vi skiller mellom to former for måling av vindskjevheter:
- Målevognkjøring
- Manuell måling
Når målevognsresulteter avdekkes overskridelser av toleransene fastsatt i forrige avsnitt, må de aktuelle stedene kontrolleres manuelt. Kontrollen foretas ved nivellering eller måling med vater. På skinnene merkes det av målepunkter for hver 2. og hver 9. meter, se figur under.
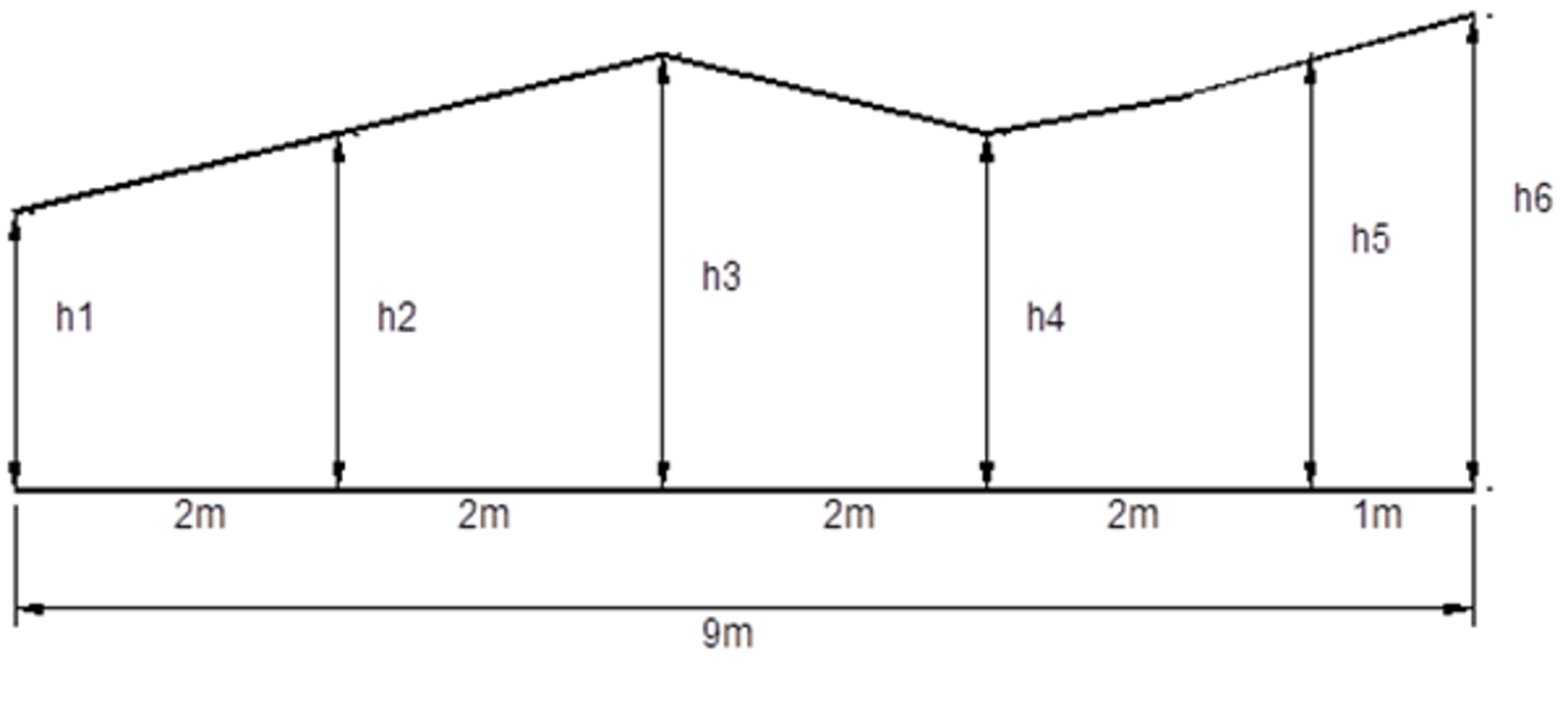
Regelverket krever at både 2- og 9-metersbasis dokumenteres og anbefaler derfor sterkt målemønsteret i figuren. Dette er en måte å få med langt på veg de fleste 2 m-feil, samt alle 9 m-feil langs strekning, uten å interpolere målinger. For kun å måle vindskjevhet vil det være tilstrekkelig å benytte et vater til måling av overhøydene for deretter å trekke ut overhøydedifferanser. Med et nivellement vil man derimot kunne si noe om vertikalkurvaturen også (til hver skinnestreng) ved å velge seg en høydereferanse for målingene.
Å måle vindskjevheter under belastning er ikke like viktig som ved sporutvidelser – som regel er vindskjevheter rimelig konstante. Men på spor som er av en slik standard at stabiliteten er dårlig, dvs. setningspartier, avsnitt med svært mangelfullt ballastprofil osv, kan store forskjeller mellom målinger på belastet/ubelastet spor forekomme. Dette fenomenet kalles da for blindslag.
1.3.2.4 Utbedring av vindskjevheter
For å unngå avsporinger som følge av for stor vindskjevhet, skal sporet være pakket omhyggelig, enten ved hjelp av maskinelt utstyr eller håndredskap. I de tilfellene justeringsarbeider må utføres umiddelbart, vil det som regel være mest aktuelt å gjøre justeringen manuelt, uten skinnegående justeringsmaskiner. Metoden for slike utbedringsarbeider er:
- justering med håndpakkeutstyr
- skoring vha. gummiplater eller treskorer
- nedgraving av forhøying som forårsaker vindskjevheten1
1 Nedgraving er en mulighet som bare kan utføres ved manuell justering. Ved maskinell justering vil de omkringliggende områdene måtte løftes i stedet til feilen blir fjernet, og dette kan raskt bli langt mer omfattende.
1.3.2.5 Høyde- og overhøydefeil
Høydefeil blir målt separat for hver av skinnestrengene og betyr kort og godt avvik fra ideell høydebeliggenhet i vertikalkurvaturen. Overhøydefeil er ujevnheter i overhøyden, altså mindre, varierende avvik fra den ideelle overhøyden over en gitt lengde. I mange tilfeller henger disse feilene nøye sammen med de feilene som også avdekkes som vindskjevheter.
1.3.2.5.1 Årsaker til feil i høydegeometri
Høydefeil oppstår som oftest samtidig med vindskjevheter. Feil i høydebeliggenheten kan gå begge veger, enten gjennom setninger pga. at underbygningen ikke er tilstrekkelig stabil, eller som forhøyninger pga. telehiv eller annet. Feil oppstår også gjerne som resultat av grov/unøyaktig justering.
Overhøydefeil har ofte en tendens til å vokse. Hvis den tilsiktede overhøyden i en kurve ikke er oppnådd ved en justering, vil belastning av sporet lett kunne påføre kurven ytterlige avvik fra ideell overhøyde.
1.3.2.5.2 Konsekvenser og toleranser
Dersom følgen av dårlig justering er for stor overhøyde, får vi et større overhøydeoverskudd E enn vi har regnet med for godstogene. Følgelig kan disse forskyve sporet så hardt innover i kurven at det ødelegger sporet. I motsatt fall blir manglende overhøyde, I, så stor for det raskeste materiellet at vi kan få en avsporing. Brå feil i overhøyden kan også gi feil i sidebeliggenhet (baks).
1.3.2.5.3 Måling av høyde/overhøyde
Overhøyde kan som beskrevet i Måling av vindskjevheter måles både med vater og med nivellement. Et nivellement kan i tillegg som beskrevet si noe om vertikalkurvaturen, dvs. stigning/fall for skinnestrengen(e). Høydefeil som målt med målevogn er derimot vanskelig å måle direkte og eksakt, men store høydefeil vil kunne avdekkes som avvik fra teoretisk vertikalkurvatur.
1.3.2.5.4 Utbedring
Høydejusteringer skal utjevne sporets variasjoner i høyderetningen med hensyn til den enkelte skinnes variasjoner i høyderetning samtidig med høydejustering.
I kurver som gjennomkjøres med liten hastighet, blir sikkerheten mot avsporing bedre når overhøyden reduseres mest mulig eller sløyfes.
1.3.2.6 Sidefeil
Sidefeil, eller baksefeil, blir som høydefeil målt separat for hver av skinnestrengene og angir avvik fra ideell beliggenhet i horisontalplanet.
Pilhøyde måles som den horisontale avstanden mellom skinnens kjørekant og midtpunktet til en 10 m eller 20 m lang korde, hvis ender følger skinnens kjørekant. I en kurve med konstant krumning skal pilhøyden også være konstant.
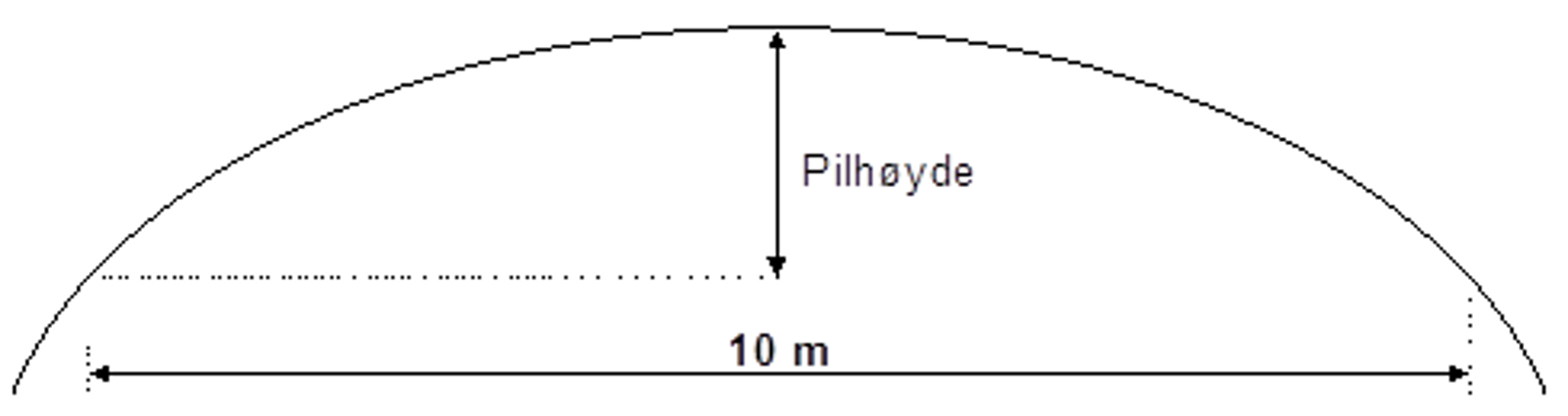
Langbølgede feil er periodiske sidefeil med bølgelengder på ca. 30 m og mer. Lange sidefeil gir små utslag i pilhøydefeil, fordi den har 10 m målebasis.
1.3.2.6.1 Årsaker til feil i sporgeometri
Brå variasjoner i overhøyden kan medføre sidefeil. Hvis sporet blir forsøkt justert ved svært lave temperaturer, blir sjelden resultatet helt tilfredsstillende, og nye sidefeil skapes.
Hvis utfestingsmetoder benyttes ved maskinell justering, og inngangsdata, sentrering e.l. er beheftet med feil, kan langbølgede sidefeil oppstå. et eksempel på dette er når sporet i en kurve har flyttet seg innover over tid og det deretter justeres til riktig avstand til VUL-merkene lengs sporet, for eksempel for hver KL-mast hver ca. 60 m. Det samme kan oppstå hvis VUL-merker, som ikke har blitt målt inn geodetisk, benyttes ved sporjustering etter at merkene av ulike årsaker har flyttet seg.
1.3.2.6.2 Konsekvenser og toleranser
En dårlig sidegeometri medfører en ubehagelig og slingrende kjøring, som igjen fører til ujevn skinneslitasje og kraftige påkjenninger for befestigelsen. Feil i sidegeometri kan også utløse solslyng. Når sidefeil blir tilstrekkelig store, oppstår som regel også en sporutvidelse samme sted.
1.3.2.6.3 Måling av sidefeil
I tillegg til pilhøydemåling med målevogn, kan sidefeil avdekkes gjennom måling med snor. Denne kan være 10 eller 20 m lang. Snora/wiren trekkes mellom to tenger som monteres over skinnehodet, og avstanden til skinnens innerkant måles midt på snora. På denne måten fremkommer pilhøyden direkte for det måleintervallet man måtte ønske – 5 m er vanlig.
Sammenheng mellom målt pilhøyde og horisontalradius.
Sammenhengen mellom målt pilhøyde og horisontalradius beregnes etter følgende formel f = a x b/2R der a = b = halve kordelengden. Snur man formelen og setter inn a = b = 5 m for 10 m korde og 10 m for 20 m korde får man følgende:
- 10 m korde: R = 12500/f
- 20 m korde: R = 50000/f
Dette gir følgende tabell for utvalgte horisontalradier.
| R | f10 [mm] | f20 [mm]) |
|---|---|---|
| 10000 | 1 | 5 |
| 5000 | 3 | 10 |
| 3000 | 4 | 17 |
| 2000 | 6 | 25 |
| 1000 | 13 | 50 |
| 900 | 14 | 56 |
| 800 | 16 | 63 |
| 700 | 18 | 71 |
| 600 | 21 | 83 |
| 500 | 25 | 100 |
| 450 | 28 | 111 |
| 400 | 31 | 125 |
| 350 | 36 | 143 |
| 300 | 42 | 167 |
| 275 | 45 | 182 |
| 250 | 50 | 200 |
| 225 | 56 | 222 |
| 200 | 63 | 250 |
| 175 | 71 | 286 |
| 150 | 83 | 333 |
| 125 | 100 | 400 |
| 100 | 125 | 500 |

1.3.2.6.4 Utbedring
Sidejusteringen skal sikre sporets nødvendige stabilitet og hovedform. Høydejustering skal alltid utføres samtidig med sidejustering.
1.4 Kvalitetsmål og justeringskrav
1.4.1 Generelle justeringskrav
I de foregående hav vi berørt en rekke konsekvenser av at ulike sporgeometriske feil overskrider visse toleranser. Når ikke helt spesifikke grenseverdier for den enkelte feilkilde er satt, gjelder generelt følgende bestemmelser:
- Ved overskridelse av tiltaksgrensene skal kvaliteten bedres snarest, senest før neste måling.
- Ved overskridelse av vedlikeholdsgrensene skal utbedring planlegges slik at feilen er utbedret senest før tiltaksgrensen kan forventes overskredet.
- De ulike toleransene innenfor disse to grenseverdiene er utrykk for hhv. preventivt og korrektivt vedlikehold av sporet. Et meget godt eksempel på viktigheten av denne avgrensningen er sporutvidelsen i avsnitt Eksempel på utvikling av sporutvidelse. Pga. at den preventive vedlikeholdet er uteblitt, dvs. varig utbedring når vedlikeholdsgrensen er overskredet, får sporutvidelsen akselerere til en tilstand som påkaller fullt sporbytte som eneste løsning.
1.4.2 Sporvurdering ved standardavvik
Gjennom målevognskjøring har det vist seg svært verdifullt å benytte standardavvik for å beskrive en serie av sporgeometrimålinger. Standardavviket σ er hyppig benyttet i statistikken for å beskrive hvordan en måleserie varierer rundt sin middellinje. Standardavviket er gitt ved:
der:
- σ = standardavvik
- n = antall måleverdier
- xi = måleverdier i mm
- xm = middelverdien av samtlige målinger
Standardavviket regnes som regel over delstrekninger på 200 m eller 1000 m.
1.4.2.1 Kvalitetsgrenser
Det er satt grenser for hvilke σ-verdier som kan sies å angi god sporkvalitet. grensene i tabell nede danner også grunnlag for beregning av kvalitetstall.
| Kvalitetsklasse | Hastighet (km/h) | Kvalitetsgrenser (mm) | |||
|---|---|---|---|---|---|
| Høydegeometri (σH) | Overhøyde (σR) | Sidegeometri (σP) | Samvirkning (σS) | ||
| K0 | 145– | 1,1 | 0,9 | 1,1 | 1,6 |
| K1 | 125–140 | 1,3 | 1,0 | 1,2 | 1,7 |
| K2 | 105–120 | 1,5 | 1,2 | 1,3 | 1,9 |
| K3 | 75–100 | 1,9 | 1,4 | 1,7 | 2,4 |
| K4 | 40–70 | 2,4 | 1,8 | 2,0 | 3,1 |
| K5 | –35 | 2,9 | 2,2 | 2,4 | 3,6 |
1.4.3 K-tallet
Kvalitetstallet (K-tallet) angir hvor stor del av en strekning der samtlige σ-verdier fra tabell over er innenfor toleransegrensene. Utrykt som ligning kan vi skrive dette som:
der:
- Σl = summen av sporlengder der alle beregnede standardavvik er innenfor kvalitetsgrensene
- L = den undersøkte sporlengden
1.4.3.1 Toleranser
Kvalitetstallet bør være så høyt som mulig. Lave verdier for kvalitetstallet vil, i tillegg til å gi redusert komfort, framskynde nedbrytningen av sporet.
| Kvalitetsklasse | Hastighet | Kvalitetstall | ||
|---|---|---|---|---|
| Nyjustert spor | Vedlkeholdsgrense | Tiltaksgrense | ||
| K0 | 145– | 90 | 90 | 50 |
| K1 | 125–140 | 90 | 85 | 40 |
| K2 | 105–120 | 90 | 80 | 30 |
| K3 | 75–100 | 90 | 75 | 20 |
| K4 | 40–70 | 90 | 70 | 20 |
| K5 | –35 | – | – | – |
1.4.3.2 Utbedring og tolkning
For undersøkelsen av grensene i tabell over gjelder de samme bestemmelsene som for sporfeil generelt, jf Generelle justeringskrav.
1.4.4 Q-tallet
I Norge er det vanlig å anvende K-tall for å angi kvaliteten på et lengre strekningsavsnitt. ROGER 1000 leveres også det såkalte Q-tallet,som også kan benyttes over kortere strekninger:
der:
- σH og σS er gjennomsnittlig standardavvik for høyde og samvirke på strekningen
- σHgr og σSgr er kvalitetsgrensene for de samme standardavvikene utfra kvalitetsklasse
Q-tallet kan variere fra negativt til 150, men avgrenses i dokumentasjonen til intervallet 0 ≤ Q ≤ 120
Forholdet mellom K-tall og Q-tall er gitt ved:
1.5 Målvognsdokumentasjon
Målevogn ROGER 1000 leverer fire ulike former for dokumentasjon:
- Målediagram
- Tiltaksfeilliste / liste over alvorlige sporfeil
- Vurderingsdiagram
- Kvalitetsliste
Mens de to øverste gjerne benyttes til å bedømme sporets tilstand ved hver enkelt måling, er de to siste ofte egnet til å analysere sporet over tid.
1.5.1 Målediagram
Selve målediagrammet (den opprinnelig dokumentasjonen) illustrerer grafisk alle størrelsene omtalt i avsnitt Sporvidde.
[1] En alvorlig vindskjevhet på 9 m basis opptrer i en fra før av bratt overhøyderampe som ender i en kurve med maksimalt overhøyde. Faktisk er overhøyden i kurven til tider over tillatte 150 mm. På overhøydekurven at rampen ikke er helt lineær.
[2] En alvorlig vindskjevhet på 9 m basis opptrer også i rampen i motsatt ende av den samme sirkelkurven. Også her ser vi at overhøydekurven at rampen ikke er helt linær. De antatte rampene er tegnet inn som stiplede, horisontale linjer. Ingen av vindskjevhetene kan imidlertid påvises å ha noe med høydefeil på noen av skinnestrengene å gjøre.
[3] Begge de etterfølgende sirkelkurvene viser typiske tegn på utvikling av en lengre og større sporutvidelse. Store deler av kurven har sporvidde godt over vidlikeholdsgrensen.
1.5.2 Tiltaksfeilliste/liste over alvorlige sporfeil
Tiltaksfeilliste, eller liste over alvorlige sporfeil for hver feil som overskrider tiltaksgrensene som gjelder for den aktuelle kvalitetsklassen:
- Type
- Størrelse
- Lengde
- Km-posisjon
Sporvidde og vindskjevhet i to målebasiser er viet hver sine kolonner i listen, på bakgrunn av deres viktighet for sikkerheten og deretter sporets kvalitet. De øvrige basisparametrene (med unntak av kurvatur, som ikke er en feil) er gjengitt i en felles kolonne.
Det er allikevel viktig å huske på at tiltaksfeillisten alene ikke alltid gir grunnlag for bedømme behovet for vedlikehold. Bruk av det grafiske diagrammet gir det mest fullstendige feilbildet.
1.5.3 Vurderingsdiagram
Vurderingsdiagrammet viser grafisk de standardavvik (over en glidende basis på 200 m) som regnes ut for de ulike parametrene. I tillegg er alle vedlikeholds- og tiltaksoverskridelser markert med en liten søyle (V og A), men disse figurerer mer som en indikasjon på hvor feilene befinner seg på strekningen. K-tall og Q-tall er også angitt for hver hele kilometer og skal leses fra høyre mot venstre.
Feilene [1], [2] og [3] er alle påvist i vurderingsdiagrammet i vedlegg 5 som søyler. Ingen av disse gir imidlertid utslag i de standardavvikene som måles.
1.5.4 Kvalitetsliste
Selve kvalitetslisten er todelt i:
- feilstatistikk: oppsummering av alle sporfeil per hele km
- sporvurdering/kvalitetsanalyse – standardavvik og utregnede kvalitetstall per km
I denne listen angis feil med lengde i meter. Her listes også overskridelser av vedlikeholdsgrensen i tillegg til tiltaksgrensene, men feilene for individuelle skinnestrenger er slått sammen til en kolonne. Listen gir ikke informasjon om tilstanden i ett enkelt traséelement.
1.6 Vedlegg: Eksempler i forbindelse med tilstandskontroll
1.6.1 Eksempel 1: Avsporing ved Fetsund stasjon
18.07.02 og 13.08.02 sporet av cargo Nets toakslede containervogner av i en overgansgkurve som strekker seg inn på Fetsund bru. Først over tre år senere, etter at Jernbaneverket tok ut stevning mot Cargo Net, ble endelig ansvar fordelt og et forlik inngått: Cargo Net ble nødt til å betale Jernbaneverket 9,5 millioner kroner pluss renter i erstatning for den første av avsporingene pga. skjevlasting av vogna som sporet av. Undersøkelser av sporgeometriske feil stod imidlertid også sentralt i begge avsporingene. I dette eksemplet skal vi se nærmere på de målingene av sporets tilstand som ble utført i tilknytning til særlig den første avsporingen i 18.07.02.
Før avsporingen var en vindskjevhet over tiltaksgrensen (>36 mm)avdekket inne på brua under periodisk målevognkjøring 27. mai 2002, samtidig med at det fantes store høydefeil, trolig pga. ustabile masser/setninger, like foran bruenden. En stund etter avsporingen ble overgangskurven nivellert.
1.6.1.1 Nivellement og justering av overgangskurve ved Fetsund 26.07.02
Data for overgangskurven:
OE:
km = 29,322
R = 289
h = 120OB:
km = 29,364
R = 0
h = 0Det ble nivellert for hver skinnestreng etter måleprinsippet 2+2+2+2+1 der tallene angir avstanden mellom målepunktene i meter. Utfra måleverdiene beregnes vindskjevheter over henholdvis 2 og 9 meter.
| Km | Målepkt. | I-streng | Y-streng | Vindskj. 2m | Vindskj. 9m | Overhøyde | Merknad |
|---|---|---|---|---|---|---|---|
| (m) | (cm) | (cm) | (mm) | (mm) | (mm) | ||
| 29 321 | 0 | 135,0 | 123,2 | 118 | Betongsville | ||
| 29 322 | 1 | 135,2 | 123,5 | 117 | OE | ||
| 29 323 | 2 | 135,3 | 123,9 | – 4 | 114 | Betongsville | |
| 29 325 | 2 | 135,7 | 124,6 | – 3 | 111 | Betongsville | |
| 29 327 | 2 | 135,9 | 125,5 | – 7 | 104 | Betongsville | |
| 29 328 | 1 | 136,1 | 126,0 | 101 | Betongsville | ||
| 29 330 | 2 | 136,1 | 126,6 | – 6 | – 23 | 95 | Betongsville |
| 29 332 | 2 | 135,6 | 126,6 | – 5 | – 24 | 90 | Betongsville |
| 29 334 | 2 | 135,4 | 126,9 | – 5 | – 26 | 85 | Tresville |
| 29 336 | 2 | 135,9 | 127,7 | – 3 | – 22 | 82 | Tresville |
| 29 337 | 1 | 136,0 | 127,8 | – 19 | 82 | Tresville | |
| 29 339 | 2 | 136,0 | 128,1 | – 3 | – 16 | 79 | Tresville |
| 29 341 | 2 | 135,5 | 128,2 | – 6 | – 17 | 73 | Tresville |
| 29 343 | 2 | 134,4 | 128,1 | – 10 | – 22 | 63 | Tresville |
| 29 345 | 2 | 133,8 | 128,5 | – 10 | – 29 | 53 | Brusville |
| 29 346 | 1 | 133,6 | 128,9 | – 35 | 47 | Brusville | |
| 29 348 | 2 | 133,4 | 129,5 | – 8 | – 40 | 39 | Brusville |
| 29 350 | 2 | 133,3 | 130,5 | – 11 | – 45 | 28 | Brusville |
| 29 352 | 2 | 132,9 | 131,0 | – 9 | – 44 | 19 | Brusville |
| 29 354 | 2 | 132,7 | 131,0 | – 2 | – 36 | 17 | Brusville |
| 29 355 | 1 | 132,6 | 131,0 | – 31 | 16 | Brusville | |
| 29 357 | 2 | 132,2 | 131,2 | – 6 | – 29 | 10 | Brusville |
| 29 359 | 2 | 131,9 | 131,4 | – 5 | – 23 | 5 | Brusville |
| 29 361 | 2 | 131,7 | 131,5 | – 3 | – 17 | 2 | Brusville |
| 29 363 | 2 | 131,8 | 131,6 | 0 | – 15 | 2 | Brusville |
| 29 364 | 1 | 131,8 | 131,7 | – 15 | 1 | OB |
Den alvorligste vindskjevheten er på hele 45 mm over 9 m basis og er større enn sikkerhetsgrensen for slike feil. Årsaken er kombinasjonen av høydefeilen før brua (humpen) og feil skording på brua.
Målingene avdekket altså en uheldig kombinasjon av høydefeil og vindskjevhet etter hverandre i sporet. Basert på nivellementet, som gir det mest eksakte bildet av situasjonen i dette tilfellet, ble fremgangsmåte for feilretting og tillemping av fornyet vertikalgeometri utarbeidet.
1.6.1.2 Strategi og framgangsmåte
- OB og innerstreng på brua ligger fast, selv om strengen likevel ikke er helt horisontal.
- Derfor innfører vi et knekkpunkt (SE) i vertikalkurvaturen i OB. Stigning 1 ‰ for å tilpasse eksisterende høyder i innestreng
- Innfører ytterligere knekkpunkter (SE) i vertikalkurvaturen for å balansere, se forklaring nedenfor
- Beregner høyde for innerstreng fram til første betongsville etter ny vertikalkurve
- Beregner nødvendig løft av innerstreng
- Beregner teoretisk overhøyde etter løfteskjema
- Beregner nødvendig løft av ytterstreng
- Beregner ny skording for brusviller
| Km | Eks. høyde I-streng | Ny teor. høyde | Nødv. løft I-streng | Teoretisk overhøyde | Målt overhøyde | Nødv. løft Y-streng | Merknad |
|---|---|---|---|---|---|---|---|
| (m) | (cm) | (cm) | (mm) | (mm) | (mm) | (mm) | |
| 29 321 | – 3,2 | – 3,5 | – 3 | 120,0 | 118 | – 1 | Betongsville |
| 29 322 | –3,4 | – 3,6 | – 2 | 120,0 | 117 | 1 | OE |
| 29 323 | – 3,5 | – 3,7 | – 2 | 117,1 | 114 | 1 | Betongsville |
| 29 325 | – 3,9 | – 3,9 | 0 | 111,4 | 111 | 0 | Nytt SE |
| 29 327 | – 4,1 | – 3,7 | 4 | 105,7 | 104 | 6 | Betongsville |
| 29 328 | – 4,3 | – 3,6 | 7 | 102,9 | 101 | 9 | Betongsville |
| 29 330 | – 4,3 | – 3,4 | 9 | 97,1 | 95 | 11 | Betongsville |
| 29 332 | – 3,8 | – 3,2 | 6 | 91,4 | 90 | 7 | Betongsville |
| 29 334 | – 3,6 | – 3,0 | 6 | 85,7 | 85 | 7 | Tresville |
| 29 336 | – 4,1 | – 2,8 | 13 | 80,0 | 82 | 11 | Tresville |
| 29 337 | – 4,2 | – 2,7 | 15 | 77,1 | 82 | 10 | Tresville |
| 29 339 | – 4,2 | – 2,5 | 17 | 71,4 | 79 | 9 | Tresville |
| 29 341 | – 3,7 | – 2,3 | 14 | 65,7 | 73 | 7 | Tresville |
| 29 343 | – 2,6 | – 2,1 | 5 | 60,0 | 63 | 2 | Tresville |
| 29 345 | – 2,0 | – 1,9 | 54,3 | 53 | Brusville | ||
| 29 346 | – 1,8 | – 1,8 | 51,4 | 47 | Brusville | ||
| 29 348 | – 1,6 | – 1,6 | 45,7 | 39 | Brusville | ||
| 29 350 | – 1,5 | – 1,4 | 40,0 | 28 | Brusville | ||
| 29 352 | – 1,1 | – 1,2 | 34,3 | 19 | Brusville | ||
| 29 354 | – 0,9 | – 1,0 | 28,6 | 17 | Brusville | ||
| 29 355 | – 0,8 | – 0,9 | 25,7 | 16 | Brusville | ||
| 29 357 | – 0,4 | – 0,7 | 20,0 | 10 | Brusville | ||
| 29 359 | – 0,1 | – 0,5 | 14,3 | 5 | Brusville | ||
| 29 361 | 0,1 | – 0,3 | 8,6 | 2 | Brusville | ||
| 29 363 | 0,0 | – 0,1 | 2,9 | 2 | Brusville | ||
| 29 364 | 0,0 | 0,0 | 0,0 | 1 | OB/Nytt SE |
1.6.1.3 Ny vertikalkurvatur
- Endringer i vertikalkurven er gjort av praktiske grunner. Hele rampen skal egentlig ligge flatt i nivå med brua.
- I virkeligheten er det en svak helling fra OB på brua tilbake til km 29,325.
- Deretter stiger det svakt tilbake mot km 29,297 som ligger på samme nivå som OB på brua.
- For å forenkle sporjusteringen legges det inn tre knekkpunkter i vertikalgeometrien.
- Stigningsendringen har liten sporgeometrisk betydning og bidrar kun til å forenkle justeringen.
- Stigningsendringen er i tillegg for liten til å kunne maskinpakkes.
| Fra km | Til km | Stigning |
|---|---|---|
| (km) | (km) | ‰ |
| 29,2826 | 29,2970 | 0,0 |
| 29,2970 | 29,3250 | – 1,0 |
| 29,3650 | 29,3640 | 1,0 |
| 29,3640 | 29,8066 | 0,0 |
Til slutt ble alle nye skordinger for brusvillene beregnet (etter måling med tommestokk), i og med at mye av feilen lå «fast» inne på brua. Alle skoringene gjengis ikke her, men det skal nevnes at avviket mellom gamle og nye skoringer utgjorde opptil 17 mm.
1.6.2 Eksempel 2: Avsporing etter sporarbeider ved Loenga/Oslo S
06.09.02 sporet et Linx-lok av tunnelen mellom Loenga og Oslo S på inngående spor på Østfoldbanen, fem dager etter endte sporarbeider 01.09.02.
Sporet ble oppgitt å være visitert daglig i mellomtiden, men aldri målt som påkrevd. Vindskjevheten ved avsporingsstedet var Norgesrekord på 2 m basis: 22 mm. Målingene nedenfor viser i tillegg at det 25 m bortenfor ville ha kommet en vindskjevhet på 55 mm på 2 m basis.
| Pkt | Profil | Avs CL | H iht. teor. SOK | H differanse | h differanse over 2 m | ‰ over 2m | h differansen over 9 m | ‰ over 9 m |
|---|---|---|---|---|---|---|---|---|
|
H169 V169 |
1196,001 1196,013 |
0,901 -0,577 |
149 241 |
92 |
-1 |
-0,5 |
||
|
H198 V198 |
1198,005 1198,005 |
0,898 -0,590 |
152 245 |
93 |
-2 |
-1 |
||
|
V200 H200 |
1200,004 1200,008 |
-0,599 0,878 |
254 159 |
95 |
-5 | -2,5 | ||
|
V02 H02 |
1202,001 1202,017 |
-0,615 0,871 |
265 165 |
100 |
-1 | -0,5 | ||
|
V04 H04 |
1204,001 1204,011 |
-0,598 0,885 |
273 172 |
101 |
-1 | -0,5 | ||
|
V06 H06 |
1206,018 1206,019 |
-0,567 0,924 |
282 180 |
102 |
3 | 1,5 | ||
|
H08 V08 |
1208,010 1208,015 |
0,933 -0,555 |
190 289 |
99 |
-3 | -1,5 | ||
|
H10 V10 |
1210,003 1210,016 |
0,895 -0,591 |
202 304 |
102 |
-2 | -1 | ||
|
H12 V12 |
1211,996 1212,008 |
0,840 -0,656 |
199 303 |
104 |
1 | 0,5 | ||
|
V14 H14 |
1214,011 1214,015 |
-0,686 0,800 |
279 178 |
103 |
55 | 27,5 | ||
|
H16 V16 |
1216,010 1216,013 |
0,780 -0,704 |
160 208 |
48 |
-42 | -21 | ||
|
H18 V18 |
1216,023 1216,023 |
0,764 -0,719 |
158 248 |
90 |
6 | 3 | ||
|
V20 H20 |
1220,121 220,14 |
-0,743 0,759 |
238 154 |
84 |
1 | 0,5 | ||
|
H22 V22 |
1222,003 1222,018 |
0,757 -0,744 |
137 220 |
83 |
-1 | -0,5 | ||
|
H24 V24 |
1224,001 1224,013 |
0,778 -0,733 |
125 209 |
84 |
-5 | -2,5 | ||
|
V26 H26 |
1226,018 1226,020 |
-0,729 0,772 |
106 117 |
89 |
-2 | -1 | ||
|
H28 V28 |
1228,017 1228,023 |
0,768 -0,732 |
118 209 |
91 |
0 | 0 | ||
|
H30 V30 |
1230,004 1230,006 |
0,768 -0,734 |
124 215 |
91 |
3 | 1,5 | ||
|
H32 V32 |
1232,010 1232,020 |
0,757 -0,743 |
123 211 |
88 |
0 | 0 | -26 | -2,8 |
|
H34 V34 |
1234,013 1234,017 |
-0,749 0,751 |
199 111 |
88 |
0 | 0 | -47,5 | -5,2 |
|
V36 H36 |
1236,007 1236,014 |
-0,753 0,757 |
193 105 |
88 |
-7 | -3,5 | -60 | -6,6 |
|
V38 H38 |
1238,000 1238,011 |
-0,755 0,766 |
199 104 |
95 |
-11 | -5,5 | -58 | -6,4 |
|
V40 H40 |
1240,015 1240,018 |
-0,744 0,777 |
217 111 |
106 |
-22 | -11 | -47 | -5,2 |
|
V41 H41 |
1241,012 1241,032 |
-0,745 0,765 |
230 116 |
114 |
-39 | -4,3 | ||
|
H42 V42 |
1242,006 1242,009 |
0,771 -0,750 |
120 248 |
128 |
-15 | -7,5 | – | – |
|
H44 V44 |
1244,014 1244,015 |
0,758 -0,744 |
135 278 |
143 |
-10 | -5 | – | – |
|
V46 H46 |
1246,011 1246,014 |
-0,745 0,767 |
286 133 |
153 |
0 | 0 | – | – |
|
H48 V48 |
1248,004 1248,029 |
0,781- 0,734 |
120 273 |
153 |
0 | 0 | – | – |
|
H50 V50 |
1250,015 1250,017 |
0,775- 0,729 |
107 260 |
153 |
– | – | – | – |
1.6.3 Eksempel 3: Blindslag på Roalinja
I juni 2001 ble en vindskjevhet på langt over 50 mm (!) på 9 m basis målt med ROGER 1000 på Roalinja i en overgangskurve på km 61,7. Da feilen senere ble forsøkt målt med vater. kunne ikke en feil av en slik størrelse gjenfinnes. Feilen som fantes her kalles et såkalt blindslag – en vindskjevhet som ikke finnes ved belastning.
Bildet over viser sporet i den aktuelle overgangskurven etter at det er forsøkt å rette opp blindslaget med påfylling av pukk og pakking av sporet (18.06.01). Som vi ser raser pukken fortsatt unna sporet f.o.m. den ytre svillehalvdelen. I avbildet tilstand ble sporet målt i begge retninger i hastighetene 20–40–60–80 km/h med ROGER 1000, og fortsatt ga hastighetene 60 og 80 km/h noen mm større vindskjevhet på 9 m basis for én av måleretningene (Roa–Grindvoll), på det meste en tiltaksfeil på 35 mm.
1.6.4 Eksempel 4: Avstanden plattformkant–tog
Et teknisk fenomen som hadde vakt stor allmenn interesse var avstanden mellom plattformkanten og persontog. For det nye dobbeltsporet mellom Skøyen og sandvika har dette fått et spesielt stort fokus allerede før spor og stasjoner er ferdig prosjektert, jf. faksimile fra Aftenpostens søndagsnummer, 16. oktober 2005. Der havnet den nye Lysaker stasjon på forsiden under denne overskriften:

Det kan være nyttig å se nærmere på hvilke faktorer som spiller inn når avstanden for ombordstigning blir så stor at det oppleves ubehagelig. Følgende teoretiske eksempel er hentet fra Hauketo stasjon på Østfoldbanen, i venstre (inngående) spor, hvor vi har en kurve med plattformen på utsiden. Figuren under viser hvordan hhv. ytre og indre kurveutslag virker inn på hvor langt fra plattformkanten sporet må ligge (inntil nylig nominelt 1700 mm til spormidt på rettlinje). Formlene for kurveutslag og bidrag fra overhøyden gås ikke nærmere inn på her, men det skal nevnes at beregningene er teoretiske i det de baserer seg på en malvogn med lengde 24 m og boggisavstand 18 m. Beregning av reel kurveutslag vil i virkeligheten variere fra togsett til togsett, samtidig med at avstanden fra tog til plattformkant for de reisende vil variere med hvor på toget dørene er plassert.
Sporet har radius R = 400 m og overhøyde h = 130 mm:
- ytre kurveutslag i vognhjørnen: Ky = 63 000 / (2*400) = 79 mm
- fratrekk for overhøyden = 28 mm
→ Kanten må bygges 1751 mm fra spormidt
- indre kurveutslag i vognmidt: Ki = 81 000 / (2*400) = 101 mm
- byggetoleranser for plattform: 0 / + 20 mm
- tillatt usikkerhet i sporbeliggenheten er + / – 20mm
- typisk (halv) vognbredde kan settes til 1550 mm (for malvogna)
→ Avstanden på det breddeste kan bli (1751 + 101 + 20 + 20 - 1550) mm = 342 mm - etter oppgitte toleranser
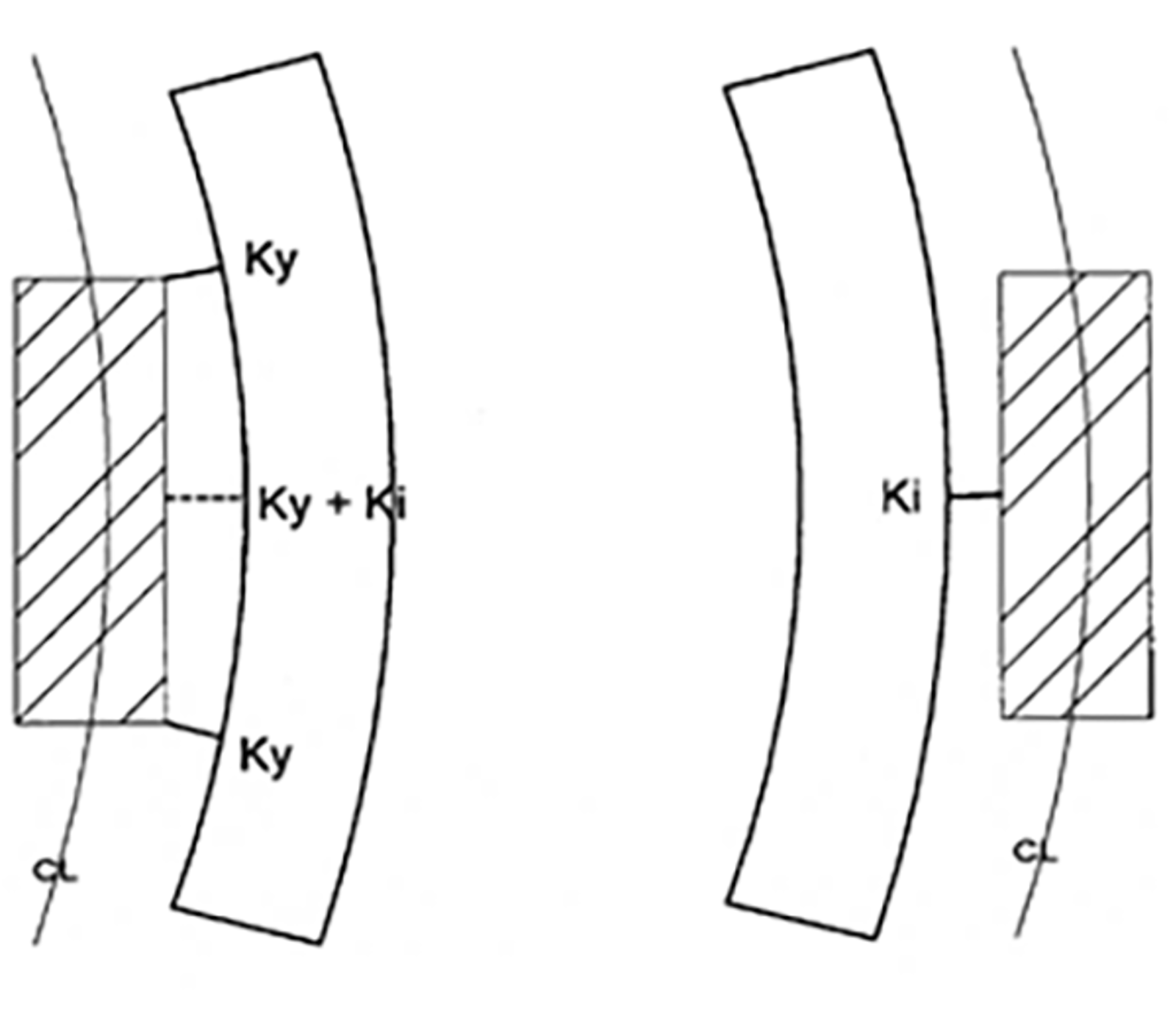
Figur 14: Figuren illustrerer hvor effekten av hhv. ytre (Ky) og indre kurveutslag (Ki) gjør seg gjeldende når vi betrakter avstanden mellom en teoretisk togvogn (skravert) og plattformkanten.
1.6.5 Eksempel 5: Målevognsdokumentasjon fra ROGER 1000
På de neste siden finnes et eksempel på målevognsdokumentasjon fra ROGER 1000 etter vårmålingen 06.06.2019 på Flåmsbana. Utsnittene er sentrert om et sporavsnitt med krappe kurver og overgangskurver med relativt bratte overhøyderamper rundt km 25, der det sist periodiske måling ble avdekket flere alvorlige sporfeil.
Dokumentasjon er hentet fra ROGER 1000s etterprosesseringsprogramvare in Office (sporgeometrianalyse) og består av følgende dokumenter:
- ca. 300 m utsnitt av sporgeometrisk målediagream
- tiltaksfeilliste
- vurderingsdiagram
- kvalitetsliste
- feilstatistikk
- kvalitetsanalyse
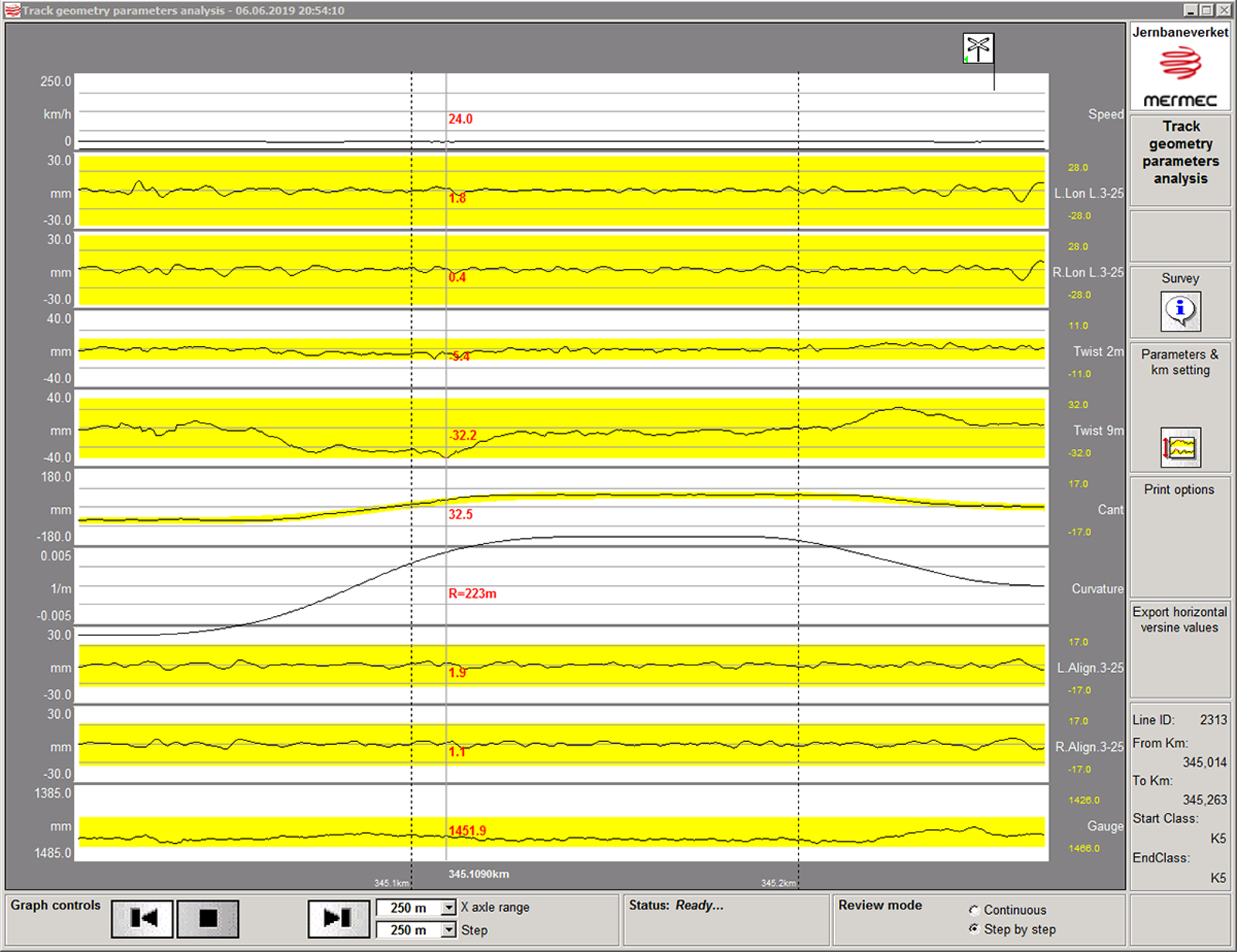
Ca. 300 m utsnitt av sporgeometrisk målediagream.
Tiltaksfeilliste
| Linje | Defekt | Klasse | Twist2 | Twist9 | Sporvidde | Km (Km) |
Breddegrad |
Lengdegrad |
|---|---|---|---|---|---|---|---|---|
| 2313 |
Vindskjevhet 2 m |
K5 | 11,9 | 335.9110 | 60.73542617° N | 7.12252089° E | ||
| 2313 | Vindskjevet 9 m | K5 | 32.5 | 335.9125 | 60.73543281° N | 7.12252083° E | ||
| 2313 | Vindskjevhet 2 m | K5 | -11.0 | 336.7990 | --.--------° | --.--------° | ||
| 2313 | Vindskjevhet 9 m | K5 | -32.5 | 345.1090 | 60.77716705° N | 7.10345656° E | ||
| 2313 | Sporvidde | K5 | 1466 | 345.6035 | 60.78032595° N | 7.09771892° E |